pari gp

Calcul de l'homologie d'une triangulation de RP^2 avec GP/PARI

Documentation en ligne de GP/PARI , et cette page pour des manuels, tutoriels, etc. Un script gp/pari peut être exécuté avec Wims ici. Une séance interactive peut être lancée avec le Sage Notebook.

Forme normale des matrices à coefficients entiers : voir la notice sur Wikipedia ou cette page.

On considère le complexe simplicial formé des 2-simplexes et de leurs faces représenté ci-dessous :

(Ce comlexe est une triangulation du plan projectif réel.) On oriente chaque simplexe de ce complexe par la numérotation indiquée des sommets du complexe. On définit dans GP/PARI les bases des groupes des 0-chaînes, 1-chaînes et 2-chaînes et les matrices des opérateurs de bord d_1 et d_2 (cf [Munkres, Elements of Algebraic Topology, chap. 1] pour une définition de ces objets). On utilise la fonction matsnf de GP/Pari pour obtenir une forme normale des matrices des opérateurs avec les matrices de changement de bases. On en déduit immédiatement une description des groupes d'homologie du complexe simplicial.

                         GP/PARI CALCULATOR Version 2.3.0 (released)
                  i686 running linux (ix86/GMP-4.1.4 kernel) 32-bit version
                 compiled: May 26 2006, gcc-4.1.0 20060304 (Red Hat 4.1.0-3)
                      (readline v5.0 enabled, extended help available)

                           Copyright (C) 2000-2006 The PARI Group

PARI/GP is free software, covered by the GNU General Public License, and comes WITHOUT ANY
WARRANTY WHATSOEVER.

Type ? for help, \q to quit.
Type ?12 for how to get moral (and possibly technical) support.

parisize = 4000000, primelimit = 500000

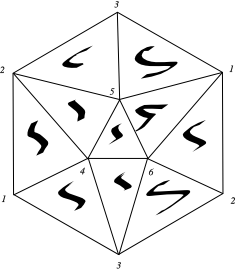
? /* Bases des 0-simplexes, 1-simplexes orientés, 2-simplexes orientés de RP^2 */
? U=[1,2,3,4,5,6];
? V=[[1,2],[1,3],[2,3],[1,4],[2,4],[2,5],[3,5],[1,5],[1,6],[2,6],[3,6],[3,4],[4,5],[5,6],[4,6]];
? W=[[1,2,4],[2,4,5],[2,3,5],[1,3,5],[1,5,6],[1,2,6],[2,3,6],[3,4,6],[1,3,4],[4,5,6]];

? /* Matrice de d_1 */
? ind(v,V)=local(i);i=1;while(V[i]<>v,i++);i /* Position de v dans V */
? A=matrix(6,15);
? for (i=1,15,A[V[i][2],i]=1;A[V[i][1],i]=-1);A /* matrice de l'opérateur de bord d_1 */
%5 =
[-1 -1 0 -1 0 0 0 -1 -1 0 0 0 0 0 0]

[1 0 -1 0 -1 -1 0 0 0 -1 0 0 0 0 0]

[0 1 1 0 0 0 -1 0 0 0 -1 -1 0 0 0]

[0 0 0 1 1 0 0 0 0 0 0 1 -1 0 -1]

[0 0 0 0 0 1 1 1 0 0 0 0 1 -1 0]

[0 0 0 0 0 0 0 0 1 1 1 0 0 1 1]

? /* rendu TeX de A */
? system("rm -f A.tex");writetex("A.tex",A);system("tex2im -r 100x100 -f gif -o A.gif A.tex");

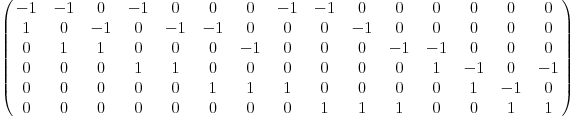
? /* forme normale de Smith */
? ?matsnf
matsnf(x,{flag=0}): Smith normal form (i.e. elementary divisors) of the matrix x, expressed
as a vector d. Binary digits of flag mean 1: returns [u,v,d] where d=u*x*v, otherwise only
the diagonal d is returned, 2: allow polynomial entries, otherwise assume x is integral, 4:
removes all information corresponding to entries equal to 1 in d.

? M=matsnf(A,1);
? M[3]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]

[0 0 0 0 0 0 0 0 0 0 1 0 0 0 0]

[0 0 0 0 0 0 0 0 0 0 0 1 0 0 0]

[0 0 0 0 0 0 0 0 0 0 0 0 1 0 0]

[0 0 0 0 0 0 0 0 0 0 0 0 0 1 0]

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]

? /* Conclusion : le noyau de d_1 est de dim 10 ; l'image de d_1 est un facteur direct de C_0 de dimension 5 */
? writetex("M2.tex",M[2]);system("tex2im -r 100x100 -f gif -o M2.gif M2.tex");

? ker=vecextract(M[2],"1..10");A*ker /* Les 10 premières colonnes de M[2] forment la matrice des coordonnées d'une base du noyau de d_1 ; vérification : */
[0 0 0 0 0 0 0 0 0 0]

[0 0 0 0 0 0 0 0 0 0]

[0 0 0 0 0 0 0 0 0 0]

[0 0 0 0 0 0 0 0 0 0]

[0 0 0 0 0 0 0 0 0 0]

[0 0 0 0 0 0 0 0 0 0]

? /* matrice de d_2 */
? B=matrix(15,10);B=matrix(15,10);{for (j=1,10,B[ind(vecextract(W[j],[2,3]),V),j]=1; B[ind(vecextract(W[j],[1,3]),V),j]=-1; B[ind(vecextract(W[j],[1,2]),V),j]=1);}

? writetex("B.tex",B);system("tex2im -r 100x100 -f gif -o B.gif B.tex");

? BB=M[2]^(-1)*B; /* Matrice de d_2 relativement à la nouvelle base de C_1 */
? writetex("BB.tex",BB);system("tex2im -r 100x100 -f gif -o BB.gif BB.tex");

? /* d_2 est bien à valeurs dans ker(d_1) ! */
? BBB=vecextract(BB,"1..10","1..10"); /* 10 premières lignes et les 10 colonnes de BB */

? N=matsnf(BBB,1); /* mise sous forme normale */
? writetex("N3.tex",N[3]);system("tex2im -r 100x100 -f gif -o N3.gif N3.tex");

? /* Conclusion : ker(d_2)={0} ; im(d_2) est de dimension 10=dim(ker(d_1)) mais n'est pas un facteur direct de ker(d_1); ker(d_1)/im(d_2)=Z/2Z */

F.X. Dehon, 11 décembre 2008, dehon@unice.fr